Causation without Correlation
Causation and correlation, while often intertwined, are distinct concepts in the realm of statistics. People often use the phrase, “correlation does not imply causation”, because when a causal relationship is present, typically correlation is present too. However, diving deeper into causal relationships exposes scenarios in which causation can indeed exist without correlation.
What is Cause?
To understand how a cause can exist without correlation, we must first understand howcauses are identified. Pearl suggests a three-step process to prove causation. The first step isassociation - understanding how variables are related. Association can be found through statistical methods such as ANOVA, regression models, and correlations. However, it is notenough.
For example, reading comprehension and kid’s shoe sizes. If someone were to gather data from K-12 students about reading comprehension and physical features, such as shoe size, a positive correlation would be present. This is because foot growth and brain development simultaneously increase, and therefore reading comprehension.
Interpreting this relationship as a cause would be incorrect. Instead, it is an effect of aging that causes both brain development and physical growth. This example demonstrates that association alone cannot define a causal relationship. That brings us to step two, intervention.
Intervention often involves experimenting in order to study the effect of change having manipulated or done something. It poses questions such as what if? and how? Referring to the shoe and reading comprehension, an example of intervention is requiring all students K-12 to have 5 more reading assignments a week. That way, an observation of how shoe size reacts to the reading change can be informative as to whether it has a causal effect. This step in causal analysis would prove that shoe size and reading comprehension do not have a casual relationship, since reading time would increase reading comprehension, but there would be no change in the pace of foot growth.
The third step is understanding the counterfactual. The counterfactual is a comparison between what happened and what would have happened. Unfortunately, a true counterfactual is impossible to observe. A counterfactual involves observing two outcomes at once. You cannot see the effect if you have not done something, but you also cannot see the potential outcome of having done so. This is called the Fundamental Problem of Causal Inference. Scientists and researchers handle this problem by collecting large samples with subjects that are closely related.
These are often called the control and effect groups. This gives the ability to identify the cause because you can see how that variable directly impacted the outcome.
Association, intervention, and counterfactuals, which all point to a cause, will result in a confident assumption of a causal relationship (Pearl). One pattern that is common to observe in causal relationships is a technique in association; correlation. Association is something that is needed to identify a cause, but it does not have to be in the form of correlation. Causation without correlation can exist in many forms.
Here are some cases.
Case 1
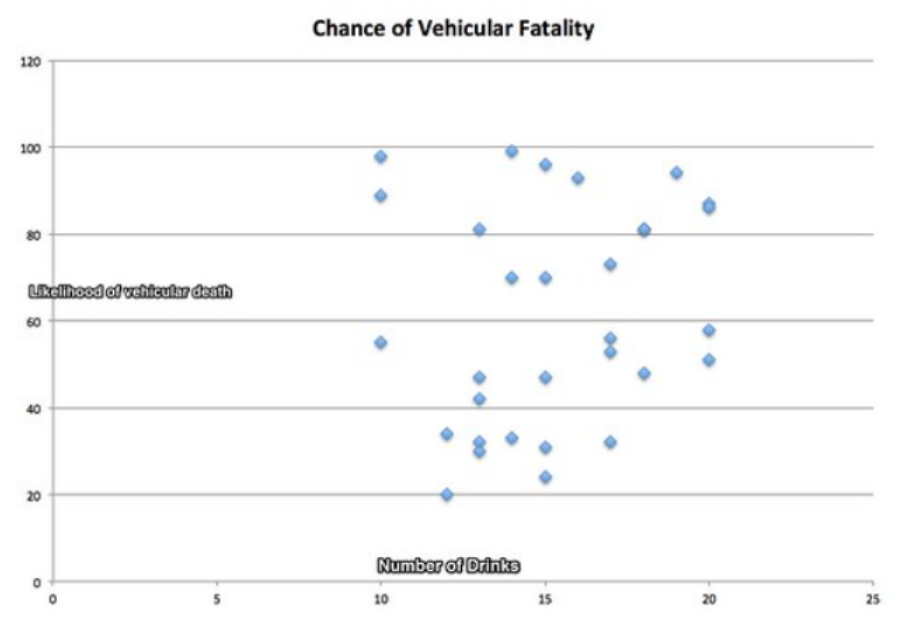
One experiment to show causation without correlation is a case that does not identify a correlation because of an insufficient sample. Take the chance of fatality from a car accident with the causal relationship to the number of drinks consumed. This has a positive correlation, because as the number of drinks consumed increases, so does the likelihood of vehicular death. However, when you plot the two variables that cause one another on a scatter plot, a visual correlation is not present.
This plot, however, only shows a population that drinks >10 per day. One cannot witness the correlation because other alcohol-related deaths interfere with the correlation pattern. Although there is a causal relationship between vehicle fatality and number of drinks, the correlation is not obvious, because of other drinking factors that also cause fatality. (Penn)
Case 2
One thought experiment to show causation without correlation is a hypothetical medical case. There is an illness that causes death, however, if they undergo treatment, they will live. Turns out that 99% of people who have the illness undergo treatment, so nearly everyone who gets ill is treated. Therefore, hardly anyone who gets ill actually dies. If we were to estimate the model without observing the treatment, then we would find that illness and death are uncorrelated, when in fact they have a causal relationship. (Frakt)
Case 3
The next case is one studied in STAT 4700. We know that force causes speed, however the two are not always correlated. Take a runner who chooses to maintain a speed of 5 mph. Their force will be constant on flat surfaces, however when the runner goes up and down hills, their force will fluctuate. As the force fluctuates the speed will continue to be maintained at 5 mph. Since one variable fluctuates while the other is constant, they are not correlated despite their causal relationship.
Case 4
This next case involves proving 0 correlation mathematically. Suppose y causes x. There is also a mediator, say B, that can take values of +1 or -1. Either outcome has an equal probability of occurring. In other words, there is a 50% chance B is +1 and a 50% chance B is -1. The equation of how the factors relate is y = Bx. When B takes on the value +1 then y = x, and when B takes on the value -1 then y = -x. The correlation for y = x is 1, and the correlation for y = -x is -1. Now, let’s say that this relationship is resampled many times to observe x, y pairs. Since the results, y = x and y = -x have an equal probability of the correlation being -1 and 1, the two outcomes end up canceling each other out and result in a correlation of zero. (Frakt)
Possible Disputes
An argument can be made that causation without correlation only occurs because the relationship is not studied enough. Specifically, that further exploration into the cause and effect variable needs to be made, and then a correlation will eventually be witnessed. This may be the case for some examples, but for some situations we may not be able to study cause and effect further. Cases with extremely small samples are confined to analysis on that sample. Additionally, knowing that correlation can exist without correlation and the other way around, helps identify suspicious claims of causation, especially with lesser studied topics.
Conclusion
Many of these cases show causation without correlation as a result of the lack of change in variables. Additionally, mediator variables or other casual variables can hide correlations. Since many people believe that causations and correlations are so tightly related, statistics can be manipulated to attempt to show a causal relationship that is not actually present. Understanding how causation can exist without correlation is important to identifying causes as well as misinterpretations.
Works Cited
Frakt, Austin. “Causation without Correlation Is Possible.” The Incidental Economist, 5 Oct. 2021, theincidentaleconomist.com/wordpress/causation-without-correlation-is-possible/.
Pearl, Judea. “An Introduction to Causal Inference.” The International Journal of Biostatistics, U.S. National Library of Medicine, 26 Feb. 2010, www.ncbi.nlm.nih.gov/pmc/articles/PMC2836213/.
Penn, Christopher S, and Name. “Can Causation Exist without Correlation? Yes!” Christopher S. Penn - Marketing AI Keynote Speaker, 25 Aug. 2020, www.christopherspenn.com/2018/08/can-causation-exist-without-correlation/#:~:text=Ca usation%20can%20occur%20without%20correlation,most%20often%20with%20insuffic ient%20samples